Random Forest

안녕하세요 데이터 과학자를 꿈꾸는 꿈쟁이입니다. 
현재 MySAS홍보대사를 수행하며 제 블로그와 MySAS E-miner활용하기 게시판에 아래와 같은 글을 동시 연재 중입니다. MySAS 게시판의 연재속도가 더 빠르니 더 많은 정보를 원하신다면 아래 링크를 이용해 주시기 바랍니다. 

나만의 SAS메뉴얼- MYSAS

www.mysas.co.kr

INTRODUCTION
랜덤포레스트는 2001년에 Leo Breiman에 의해 처음으로 소개된 기법으로 의사결정 트리의 단점을 개선하기위한 알고리즘 중 가장 지배적인 알고리즘의, 하나로 다수의 의사결정 나무를 결합하여 하나의 모형을 생성하는 방법 중 하나입니다. 기존의 앙상블 모형과의 가장 큰 차이는 임의성(randomness)를 관측치(observation, instance)뿐만 아니라 변수(feature, variable)에도 적용했다는 것입니다. 
 
RANDOM FOREST -LITERATURE REVIEW
앞서 소개 했듯 랜덤포레스트는 기존의 배깅 방법에 각 붓트스트랩 셈플의 변수에 임의성을 더한 방법입니다. 따라서 기존의 배깅모형보다 더 다양한 초평면(hyperplane)을 갖게 되고 결과적으로 앙상블 이론이 갖는 장점을 극대화하여 예측 및 분류 정확도를 기존의 방법보다 개선하며 안정성을 얻게 됩니다. 
 
이렇게 우수한 성능을 나타내게 되는 배경에는 의사결정나무의 큰 특징인 불안정성이 작용합니다. 의사결정 나무의 경우 표본 및 변수에 따라 모형의 변화폭 및 예측력의 차이가 매우 심하게 나타나는 즉 불안정성이 매우 큰 모형 중 하나입니다.
 
이러한 특징을 이용해 의사결정 나무의 표본의 개수를 조정함으로써 다양성을 확보하는 것이 가능하고 이러한 점을 이용한 것이 배깅입니다. 하지만 이 방법의 경우 지배적인 변수가 포함 되어 있기 때문에 뿌리 노드가 변하지 않아 트리가 유사한 형태로 학습됩니다. 이렇게 될 경우 트리의 다양성이 비교적 떨어져 앙상블 모형의 장점을 극대화 하는 데에는 한계가 있습니다.
 
PROS AND CONS
랜덤포레스트의 경우 위에서 언급한 것과 같이 다양성을 극대화 하여 예측력이 상당히 우수한 편이고 배깅과 동일하게 붓트스트랩 표본을 이용한 다수의 트리의 예측 결과를 종합하여 의사결정을 진행하기 때문에 안정성도 상당히 높다는 장점이 있습니다. 하지만 랜덤포레스트 역시 다수의 트리를 이용한 의사결정 기법을 이용하기 때문에 기존의 트리가 갖는 장점 중 하나인 설명력을 잃게 된다는 단점이 존재합니다.
 
CRITICAL OPTIONS
일반적으로 랜덤포레스트 모형의 핵심적이 옵션으로는 각 붓트스랩 샘플에서 이용한 변수의 개수와 하위 트리의 개수 정도가 매우 중요하게 작용합니다. 또한 개별 트리의 깊이의 경우 배깅과 마찬가지로 최대한 깊게 만드는 것이 좋다고 알려져 있습니다. 
 
일반적으로 선택변수의 개수는 전체 변수의 수의 제곱근을 많이 이용합니다. 일반적으로 이렇게 선택하는 것이 좋은 예측력을 나타내는 것으로 알려져 있습니다. 하지만 변수의 수가 방대한 경우 선택 변수의 수를 줄이는 것이 더 좋다고 알려져 있습니다. 
 
ALGORITHM

SETTING
랜덤포레스트의 세부적인 알고리즘은 위와 같습니다. 위에는 명시되어 있지 않지만 우선 데이터를 학습용(Train)데이터와 평가용(Validate)데이터로 분할합니다. 이 때 학습용 데이터를 L이라 하고 이 데이터는 총 n개의 관측치를 갖는 다고 합니다. 이 때 Ly는 각각의 class member를 의미하는데 즉 학습용 데이터에서 붓트스트랩 샘플링 기법에 의해 추출 된 y번째 데이터를 의미합니다. 그 다음 B의 경우 랜덤포레스트 생성에 이용할 총 하위 트리의 수를 의미합니다. 
 
FLOW CHART

PROCEDURE
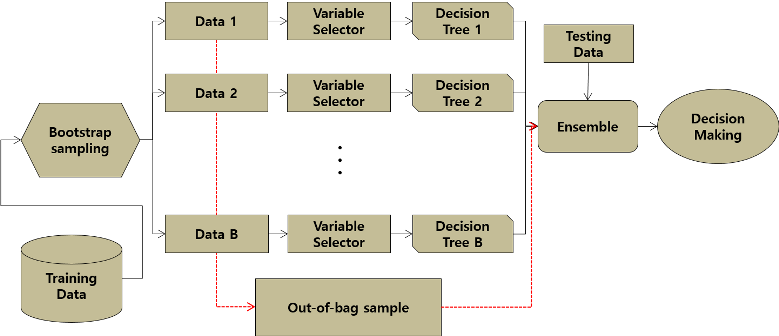
우선 학습용 데이터로부터 총 B개의 하위 데이터 셋을 붓트스트랩 샘플링을 통해 생성합니다.  그 다음 이렇게 생성된 각 샘플에서 sqrt(p)또는 p/3개의 변수를 랜덤하게 추출하고 나머지 변수는 모두 제거합니다(p : 전체 변수의 수, 위 알고리즘 상에서 전체 관측치의 수와 동일하게 n을 사용하고 있어 변경함). 이렇게 생성된 총 B개의 하위 데이터 셋들을 이용해 B개의 트리모형을 학습시킵니다. 최종 모형은 위와 같이 학습된 총 B개의 모형의 의사결정 결과를 종합하여 최종 집단혹은 값을 예측하도록 합니다.
 
Out-Of-Bag(OOB)
Oob 샘플은 위 흐름도에서 붓트스트랩 샘플링 과정에서 추출되지 않은 관측치들을 말하며 이 샘플들은 주로 평가용 데이터에서의 오분류율을 예측하는 용도 및 변수 중요도를 추정하는 용도로 많이 이용됩니다.
 
CONCLUSION
이번 연재에서는 매우 많이 쓰이는 앙상블 모형 중 하나인 랜덤포레스트 기법에 대해 알아봤습니다.랜덤포레스트는 기존의 배깅 방법에 변수임의화를 더한 방법으로 예측력과 안정성을 동시에 확보할 수 있는 장점이 있었습니다. 반면에 해석이 불가능 하다는 단점이 존재했습니다. 랜덤포레스트 방법에서의 가장 핵심적인 옵션으로는 하위 트리의 개수 및 랜덤 선택 변수의 수가 있었습니다. 일반적으로는 sqrt(p)개가 많이 이용되지만 변수의 수가 많은 경우에는 이 숫자를 줄이는 것이 좋다고 알려져 있습니다. 그 외에도 붓트스트랩 샘플의 특징에 의해서 이용하지 않는 샘플인 Out-Of-Bag 샘플에 대해서도 알아 보았습니다. E-miner의 경우엔 OOB샘플을 이용해 모형의 오차 및 각 변수의 중요도를 평가하는 데에도 이용합니다. 그럼 오늘 연재는 여기서 마무리 하도록 하고 다음 시간에는 오늘 알아본 랜덤포레스트 방법을 E-miner를 이용해 구현하는 방법에 대해 알아보도록 하겠습니다.

REFERENCES
[1] R, SAS, MS-SQL을 활용한 데이터 마이닝 / 자유아카데미 / 이정진 지음
[2] An introduction to statistical learning / Springer / Gareth James 외 3명
[3] Leo Breiman October 2001 Volume 45, Issue 1, pp 5-32. “Random Forests - Machine Learning.” 
[4] Department of Statistics CMU Rebecca C. Steorts “Bagging and Random Forests” March 18 2014. http://www.stat.cmu.edu/~rsteorts/slides/slides_lecture15.pdf  
[5] Miguel Maldonado, Jared Dean, Wendy Czika, and Susan Haller. 2014. “Leveraging Ensemble Models in SAS® Enterprise Miner™.” Proceedings in SAS Global Forum 2014.

[ 출처 ] https://m.blog.naver.com/gksshdk8003/220914969026